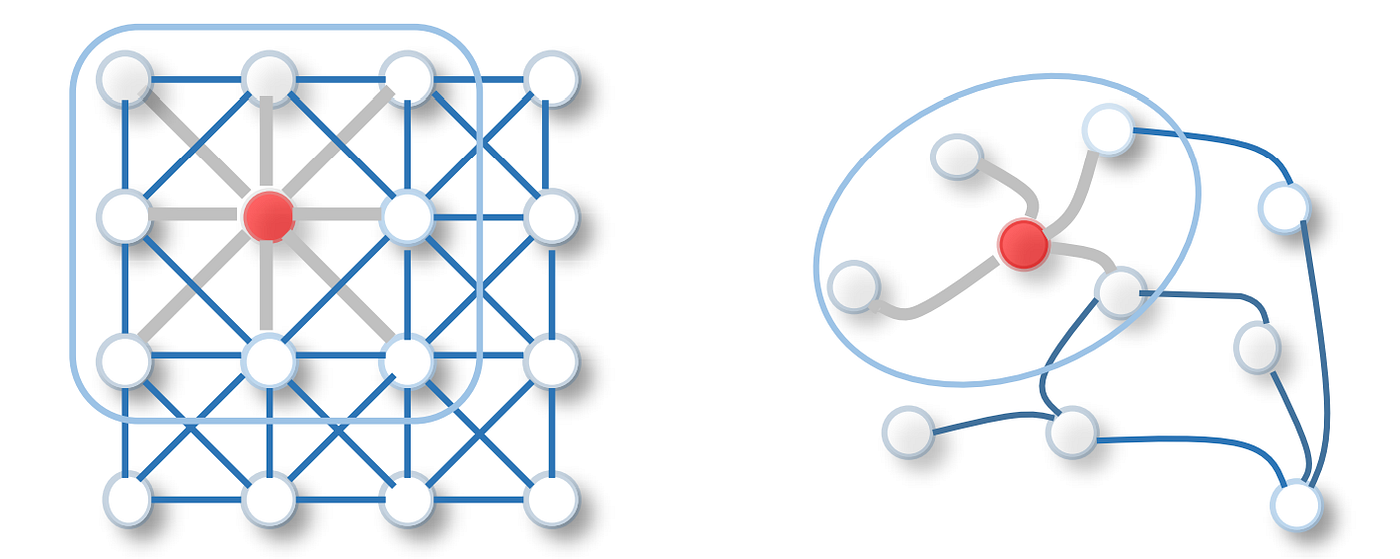
Imagine trying to spread ripples across a lake. When you toss a pebble into calm water, the waves expand smoothly and evenly. But what if the surface isn’t flat what if it’s dotted with islands, reeds, and uneven currents? That’s what working with graphs feels like in the world of data. Traditional neural networks thrive on grid like data, like pixels in an image or words in a sentence. But when information exists in irregular webs such as social networks, molecular bonds, or transportation gridsthe waves of learning behave differently. Graph Convolutional Networks (GCNs) are the ingenious solution that lets those ripples travel through complex, uneven waters.
Beyond the Grid: The Challenge of Irregular Data
Deep learning’s early success stemmed from patterns that were easy to map. A convolutional neural network (CNN) could scan an image because every pixel had clear neighbours. But in a graph, there’s no tidy order. One node might connect to hundreds of others; another may only link to one. The challenge lies in understanding how influence flows in this uneven terrain.
Think of a bustling city where some neighbourhoods are tightly knit while others sprawl loosely at the edges. Each district each node shares information differently. A GCN learns how to respect these varying relationships, passing knowledge along the city’s intricate streets instead of simple straight lines. Learners in a Data Science course in Delhi often encounter this very concept when studying how to make sense of data that defies conventional shapes and boundaries.
The Pulse of Information Flow
In essence, a GCN asks: “How does one node affect another?” Instead of scanning evenly spaced pixels, it propagates signals through edges that act like telephone lines between friends. Each node updates its knowledge by listening to its neighbours and adjusting its understanding accordingly. The key lies in the convolution a process that aggregates, weights, and blends the information from nearby nodes.
To visualise it, imagine each node as a musician in an orchestra. The melody isn’t carried by one instrument alone but shaped by how each player hears and responds to others. The conductor the GCN’s mathematical framework ensures harmony by blending local sounds into global music. The result? A model that understands the symphony of complex data networks, even when no two instruments are equally connected.
How GCNs Learn: The Mathematics of Message Passing
Under the hood, GCNs rely on the principle of message passing. Each node gathers information from its neighbours, transforms it through a shared function, and updates its own representation. Over several layers, this repeated process helps the network capture both local and global structure.
Imagine a chain of gossip in a crowded café. You tell two friends a secret; they whisper it to theirs, and soon, everyone has a slightly altered version. By the time the rumour spreads across the room, it carries traces of every voice it passed through. Similarly, each GCN layer captures broader context first, nearby relationships, then communities, and finally the entire network.
In practice, these operations use adjacency matrices, normalisation, and activation functions, yet the intuition remains elegant: learning from your neighbours to become wiser yourself. Professionals studying in a Data Science course in Delhi discover that this concept isn’t confined to graphs it reflects a universal truth of data learning: context amplifies understanding.
Applications: From Molecules to Markets
The magic of GCNs lies in their versatility. Chemists use them to predict molecular properties by analysing atom connections. Social media analysts use them to detect fake accounts or recommend friends by examining interaction graphs. In finance, GCNs uncover hidden patterns in transaction networks to prevent fraud. Urban planners deploy them to optimise transport flows by studying how people and vehicles move through city nodes.
Think of GCNs as detectives following clues through a maze. Instead of walking straight roads, they crawl along alleys, bridges, and tunnels discovering relationships invisible to models that demand order. This flexibility turns irregular chaos into meaningful structure, making GCNs indispensable in domains where relationships matter more than raw features.
Why GCNs Represent the Future of Connected Intelligence
Traditional machine learning models treat data points as isolated islands. GCNs, in contrast, recognise that knowledge exists in relationships. They bridge the gap between local detail and global insight, making sense of how entities influence one another.
This relational intelligence mirrors how humans learn. We don’t memorise facts in isolation; we connect them into webs of meaning. When one idea sparks, it triggers associations in others just like nodes activating in a graph. As systems become more interconnected, from smart cities to IoT ecosystems, GCNs provide the mathematical language to capture those interdependencies. They embody a shift toward models that not only process data but understand the networks shaping it.
Conclusion
Graph Convolutional Networks bring order to the chaos of irregular data. They translate the disciplined rhythm of CNNs into the free-form language of graphs, letting machines interpret webs of relationships as naturally as they once read pixels or words. By learning how to pass messages, combine knowledge, and detect patterns across unpredictable connections, GCNs empower us to model the world’s most complex systems.
In a landscape where everything from molecules to markets is linked, understanding those links becomes the key to intelligence itself. GCNs are not just another algorithm; they’re a bridge between structure and meaning. And for the next generation of data professionals, mastering them may well define the future of connected discovery.